【3】机器人手眼标定：固定向下相机

相机固定向下安装是手眼搭配中最简单的应用模式，也是大家最常用，最容易理解的一种方式。就让我们从这种简单的应用场景一起思考其中的一些奥妙吧。— Edited By Hugo

前言：在各种项目应用场景中，我们通常都是对着已有的公式输入原始数据，执行函数得出结果。得益于良好的封装性，函数里面发生了哪些事情却不太清楚，但有一些同学总是保留了良好的求知欲,殊不知，可能会发现一片更宽阔的知识海洋。

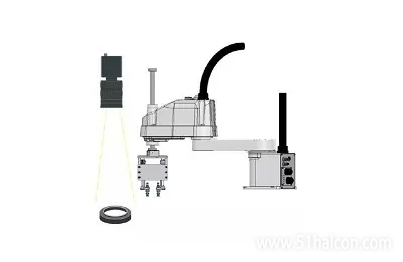
如上图所示：要让机器人的手抓住杯子，就必须知道杯子跟手的相对位置关系，而杯子的位置则是通过机器人的眼睛看见的，所以，我们只需要知道机器人的手可以眼睛的转换关系，就可以随时抓取机器人眼睛所看到的物体了。
先演示下相机标定过程：
STEP 1:准备好一张标定板，里面有3X3的圆。

STEP 2:把标定板水平放置在相机正下方，控制相机拍照得到一张图片，并按顺序（走Z字型）记录图片上9个圆的中心位置。

STEP 3:控制机器人TCP工具末端按顺序（走Z字型）移动到每个圆心，并记录下9组机器人位置坐标数据。
STEP 4:执行标定，这里使用HALCON标定算子作为演示，利用上面求得的数据。
  -图像上9个位置-

1. image_x:=[727.884,2395.058,1505.023,666.948,2678.36,1505.023,666.948,2678.36]
   
2. image_y:=[755.759,664.057,1289.824,1787.698,1707.432,1505.023,666.948,2678.36]

复制代码

  -机器人9个位置-

1. robot_x:=[-57.011,-33.521,-46.759,-58.678,-30.024,-46.759,-58.678,-30.024]
   
2. robot_y:=[323.965,324.565,316.237,309.794,309.695,-46.759,-58.678,-30.024]

复制代码

  -图像与机器人数据结合-

1. vector_to_hom_mat2d (image_x, image_y, robot_x, robot_y, HomMat2D)

复制代码

STEP 5:标定完成后，拍摄一个特征点的，求得像素位置

1. img_x:=2094.344
   
2. img_y:=1326.878

复制代码

利用以下算子即可把像素坐标转换成机器人坐标

1. affine_trans_point_2d(HomMat2D,img_x,img_y, Qx, Qy)

复制代码

到这里标定以及转过程就完成了。是不是觉得很简单？那么问题来了，他怎么做到的呢，这个标定函数里面做了什么？下面一起看看：

如上图所示：

矩阵A代表了图像像素点的点集合，矩阵B代表了机器人在世界坐标系下的点集合，在机器人应用中，我们习惯使用齐次坐标与齐次矩阵来统一描述刚体的位置和姿态。而X就是我们需求出的AB两组点集之间的旋转平移关系矩阵。
在做平面手眼标定（非3D）时，都是利用该等式进行求解的。这也是我们通常熟悉的N点标定的数学原型。这也无论是四轴机器人还是六轴机器人（姿态固定）都同样适用。
听到矩阵两个字是不是很烦？没关系你看看这个两个等式就很容易明白了。  

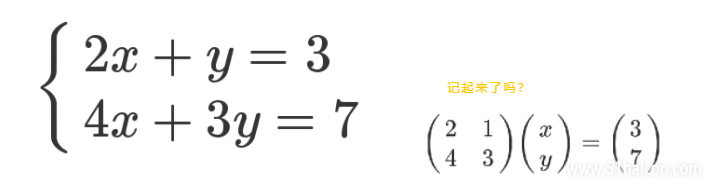
矩阵最开出现的目的在于简化线性方程的写法。矩阵的本质就是线性方程式，两者是一一对应关系。
为何图像与机器人的标定关系可以这样来表示呢？
我们知道，三维空间中的一个平面可以使用一个三元一次方程来表示，所以在平面标定中，假设图像坐标系为A平面，机器人坐标系为B平面。那么通过三元一次方程组，可求出一个平面分别与AB平面相交。可表示如下：

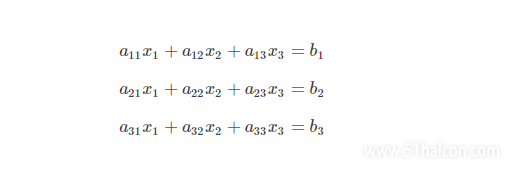
当使用N组数据时，即可使用点集A*矩阵R=点集B的方式进行表示了。这个矩阵R矩阵我们通常称为仿射变换矩阵。

仿射变换（Affine Transformation）是空间直角坐标系的变换，从一个二维坐标变换到另一个二维坐标，仿射变换是一个线性变换，他保持了图像的“平行性”和“平直性”，即图像中原来的直线和平行线，变换后仍然保持原来的直线和平行线，仿射变换比较常用的特殊变换有平移(Translation)、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切(Shear)。

已知给定两个对应点集AB，如何估计指定变换矩阵R的参数？
一对对应点可以列两个线性方程，多个对应点可以列出线性方程组，为了求解参数，需要的对应点数至少为自由度的一半，多个点时构成超定方程组，可以基于最小二乘或者SVD分解等方法进行求解，这里就暂时展开讨论。


关于SVD求解过程可参考下面连接：
https://blog.csdn.net/chenaiyanmie/article/details/80011244
在实验过程中遇到问题的或者存在疑问的
可以关注后联系我~

感谢分享，来学习了，楼主可否讲讲流水线动态抓取思路

只有八个点的数据

rencaiwang 发表于 2020-7-17 22:32
感谢分享，来学习了，楼主可否讲讲流水线动态抓取思路

动态抓取 对于视觉来说都是一样的  对于机器人来说就是获取触发信号和坐标数据 只要把机器人这端的跟踪标定做完就可以了

感谢大佬的细心讲解，顶顶顶！！！！！！！

干货啊，讲解的还是比较细致的。结合动画之后，效果更是非常的明显

相机是固定的，还是移动的？固定的怎么移动9个点，没看明白。

问一下，一个圆机械手走9点，拍9张，有9个图像坐标可以吗？
你这一个图像9个点用的哪个坐标？看公式不是全用啊？

是给的坐标不对吗，还是哪里问题，试了帖子中给的坐标，计算出放射矩阵后，在输入原来九点用任意一个相机的坐标点，但是得出的机械手坐标点与原来输入的并不一直呢

这个方法亲测有用，很好，但是精度只能到0.3mm，有办法优化吗